Codeforces Round 910 (Div. 2)
A
如果B的数量比k多,那么把在前面的B全部改成A就行了。如果B的数量少于k,那么A的数量一定多于n-k,把AB反转做同样的操作即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n, k, cnt = 0;
cin >> n >> k;
string s;
cin >> s;
for (char c : s) {
cnt += c == 'B';
}
if (cnt == k) {
cout << "0\n";
return;
}
if (cnt > k) {
for (int i = 0; ; ++i) {
cnt -= s[i] == 'B';
if (cnt == k) {
cout << "1\n" << i + 1 << " A\n";
return;
}
}
}
k = n - k;
cnt = n - cnt;
for (int i = 0; ; ++i) {
cnt -= s[i] == 'A';
if (cnt == k) {
cout << "1\n" << i + 1 << " B\n";
return;
}
}
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
int t;
// scanf("%d", &t);
cin >> t;
while (t--) {
solve();
}
return 0;
}
|
B
显然要使得分裂次数最少,最后一个数肯定是不能分裂的。前面的数要是比后面的数大就一定要分裂。显然同一个数分裂次数最少,分裂后最靠前的数最大时最优。于是若后一个数是x,前一个数是y,y > x,则y应该分裂成ceil(y / x)个数,其中最前面的一个数是floor(y / x)(因为要单调不降,余数放后面)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+5;
int a[N];
void solve() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
int x = a[n];
ll ans = 0;
for (int i = n - 1; i >= 1; --i) {
int y = a[i];
if (y <= x) {
x = y;
continue;
}
int p = (y + x - 1) / x;
ans += p - 1;
x = y / p;
}
printf("%lld\n", ans);
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
int t;
// cin >> t;
scanf("%d", &t);
while (t--) {
solve();
}
return 0;
}
|
C
容易想到消耗步数的方式是在一个2x2的四条边上绕圈。设左上到右下的曼哈顿距离为t(其实就是m + n - 2),当k - t模4余数为0时可以无成本绕圈,余数为2时可以在某处浪费掉两步,余数为1或者3时可以证明无解。构造时在左上角绕圈,在右下角提供浪费两步的结构就可以用一种构造方式解决所有问题。
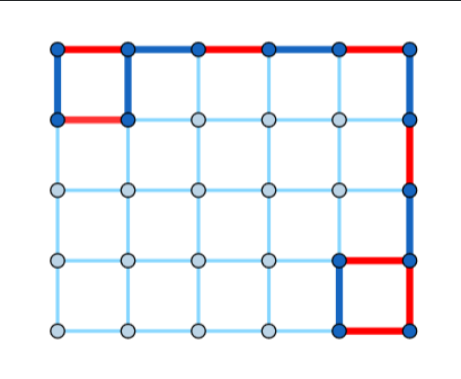 构造示意图
构造示意图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
int t = n + m - 2, s = (k - t) % 4;
if (k < t || s & 1) {
printf("NO\n");
return;
}
printf("YES\n");
bool a1[20][20] = {0}, a2[20][20] = {0};
a1[2][1] = 1;
for (int i = 1; i < m; i += 2) a1[1][i] = 1;
for (int i = m & 1 ? 1 : 2; i < n; i += 2) a2[i][m] = 1;
int o = a2[n - 1][m];
a2[n - 1][m - 1] = !o;
a1[n - 1][m - 1] = a1[n][m - 1] = o;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j < m; ++j) {
printf("%c ", a1[i][j] ? 'R' : 'B');
}
printf("\n");
}
for (int i = 1; i < n; ++i) {
for (int j = 1; j <= m; ++j) {
printf("%c ", a2[i][j] ? 'R' : 'B');
}
printf("\n");
}
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr); cout.tie(nullptr);
int t;
// cin >> t;
scanf("%d", &t);
while (t--) {
solve();
}
return 0;
}
|
E
因为字典序大的字母无法移动到在它之前且字典序比它小的字母前面,于是考虑贪心做法,对于t中的每一个字符,在s中找到第一个相同的字符,并且删掉这个字符以及它前面比它字典序小的字符(在前面且字典续大的字母可以交换到后面来)。
实现时对每一个字符构造一个以在s中出现位置为元素的队列,模拟过程中将删除的字符全部出队。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
bool solve() {
int n, m;
string s, t;
cin >> n >> m;
cin >> s >> t;
vector<int> q[26];
int p[26] = {0};
for (int i = 0; i < n; ++i) {
int x = s[i] - 'a';
q[x].push_back(i);
}
auto fnd = [&](vector<int> &a, int l, int x) -> int {
int r = a.size() - 1;
while (l < r - 3) {
int m = (l + r) / 2;
if (a[m] > x) r = m;
else l = m + 1;
}
for (int i = l; i <= r; ++i) {
if (a[i] > x) return i;
}
return a.size();
};
for (char c : t) {
int x = c - 'a';
if (p[x] == q[x].size()) return false;
int y = q[x][p[x]];
++p[x];
for (int i = 0; i < x; ++i) p[i] = fnd(q[i], p[i], y);
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t;
cin >> t;
// scanf("%d", &t);
while (t--) {
printf(solve() ? "YES\n" : "NO\n");
}
return 0;
}
|
如果字符集也为2e5规模,可以用线段树维护队列头部指针,因为更新时是所有字典序小于某个字符的队列指针位置都要移动到某个数后面。
